摘要:利用有限元理论和软件对典型的钢筋混凝土刚架拱桥建立了空间结构分析模型,对其空间结构性能,尤其是横向联系的内力进行了分析计算,并与传统的设计理论———弹性支承连续梁简化方法进行比较分析,最后用典型的桥梁进行实验研究和论证。结果表明该结构桥梁的横向联系设计合理与否,直接关系到结构的整体受力与安全,是影响其承载力的重要因素,在设计分析中应引起足够的重视.

0 引言

钢筋混凝土刚架拱桥在我国部分地区占有相当大的数量,且一般建成运营时间较长,部分已产生较为严重的病害,其中较多的或是拱脚发生位移导致拱顶实腹段区域开裂、产生马鞍形的变形,或是横向联系刚度较小、配筋不足、造成横隔板(梁)严重的开裂甚至发生断裂。究其原因,一方面刚架拱桥属推力结构,在长期的推力作用下,由于地基土壤将会发生一定的固结塑性变形,从而导致拱脚向外侧水平移动,造成拱顶产生较大的附加弯矩和下沉;另一方面,由于以往的设计理论一般采用弹性支承连续梁简化法来计算结构荷载在横向的分布和纵向的内力,而对结构 的横向联系构件(梁或隔板)计算分析,由于受到计算理论和手段的限制,或不予计算,或按工程师的直觉判断进行构造配置,设计存在很大的盲目性和随意性,致使这种桥梁结构的横向联接刚度和强度得不到保证。因此,分析研究这种桥梁结构的结构性能及横向联系的内力,对于合理指导桥梁的设计及加固,具有重要的理论意义和工程实用价值。本文的工作是应用空间有限元分析刚架拱桥的结构性能,重点分析了横向构件的受力状况,并与传统的弹性支承连续梁简化方法进行比较分析,最后用典型的桥梁进行实验研究和论证。

1 工程背景

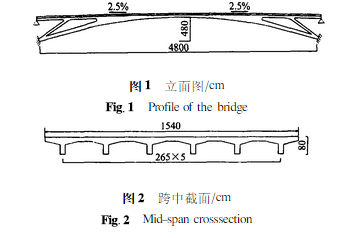
为了分析研究刚架拱桥结构的空间结构性能及横 向联系的内力,本文选取一座净跨径48m的钢筋混凝土刚架拱桥,矢跨比为1/10。该桥横向采用6片拱肋布置,单片肋宽32cm,肋间距2.65m,在主拱腿部每两根肋间共用6道横梁连接,并在全跨的实腹段及次梁桥面系结构设置11道横隔梁(包括桥端部),其中实腹段每隔4m设一道,间距在次梁段扩大(桥梁立面及跨中截面如图1、2所示)。桥梁次梁段上弦杆端支座采用板式橡胶支座,拱脚基础为埋置式沉井加阻滑板形式的基础。桥梁采用少支架施工,预制拱肋,拱肋、腹杆、上弦等主要受力构件采用C30混凝土。设计荷载汽-20级、挂-100。

2 空间结构模型的建立

2.1 建模的基本原则

本研究结构计算采用通用有限元软件Ansys。空 间建模的基本要求是在硬件条件允许的情况下尽可能的精确模拟结构物,以满足实际需要。作为工程分析,该桥模型材料采用线弹性假定;考虑到桥梁的设计构造特点,单元选用多种单元形式来构建,对微弯板、拱架及横系选用板单元,对桥面铺装选用块体单元,而横隔梁则选用梁单元。不同单元的互相连接采用共用节点及自由度耦合。对于桥上附属结构如栏杆等,由于对结构刚度影响很小,以附加质量的形式模拟在与其相连的构件上。边界条件为:拱角处固支;上弦杆端约束竖向及横桥向位移。桥梁的有限元模型共1.7万个单元,整体有限元分析模型见图3。

2.2 横隔梁的模拟

该桥横隔梁宽20cm,高45～61cm,其顶面与桥面连接良好(预留钢筋浇注)。为实现横隔梁的精确模拟,选用梁单元(Beam188单元,铁木辛科梁,适合短高梁;若选用板单元,则在微弯板与横隔梁的连接处受板厚影响,很难准确模拟),并采取自由度耦 合、单元偏置等方法,明确地模拟横隔梁的受力特征。横隔梁在桥梁横向由拱架分割为5段,在有限元模型中,每段又分为6个单元,见图4。单元偏置及梁板耦合关系见图5横隔梁与微弯板单元节点耦合关系图。在图中,由于梁单元轴线实际位置并不在一条直线上,必须通过单元偏置来模拟真实情况。横隔梁两端的节点与桥面系及拱架共用节点,在中间的5个节点采用耦合及耦合方程与其在y方向上对应的板单元节点建立联系。取图5中的节点1与其在y方向上对应的板单元节点2为例。

2.3 计算加载

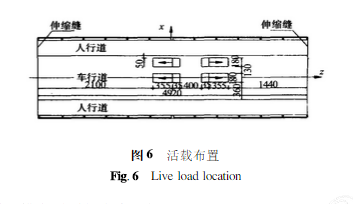
计算荷载根据桥梁的设计荷载标准,选用4辆 300kN重的加重车(前轴重60kN,中轴重120kN,后轴重120kN,轴距135cm和350cm)模拟设计荷载汽-20级、挂-100的最不利内力进行布载,车辆的横向 间距按桥梁规范,具体布置见图6。在计算中,模型的加载以节点力的形式加载在桥面上,一个轮重作为一个节点力。

3 横向联系的内力分析

通过模型结构计算,该桥的最不利构件为横隔梁。

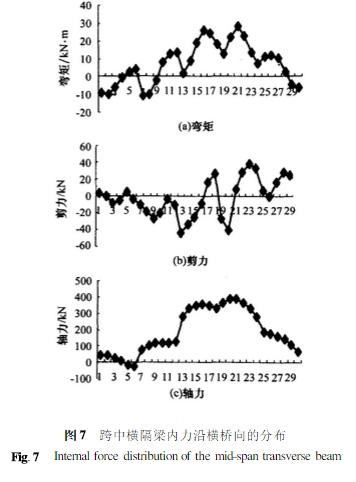
在相当设计荷载作用下,跨中横隔梁内力计算结果见图7。图中横轴代表横隔梁横向单元序号,共30个单元,序号按x轴正方向升序排列。

横隔梁的荷载及约束条件是复杂的,因而内力分布也是一组复杂的曲线。弯矩、轴力曲线都是在横隔梁与拱架的节点处有突变;剪力由于受加载影响,在加载点处表现出明显的特征。弯矩、轴力的分布图直观的反映出横隔梁的受力状况,是与实际结构受力状况相符合的。

综合面内弯矩、轴力的计算值,4#横隔梁上的21#单元是跨中横隔梁的最不利位置,见图7,截面最大拉应力σmax=6.10MPa,该单元截面荷载:弯矩M=28.23kN・m,轴力F=388.42kN。若根据现有的 横隔梁截面尺寸宽b=20cm、平均高度h=59.9cm进行配筋复核,不难发现该截面配筋明显不足,截面尺寸也不够,这一点在后续的荷载试验研究中得到了验证。

4 横向联系刚度对横向分布的影响及比较

    为进一步研究分析横向联系对整桥受力特征及横向分布的影响,本研究中将原计算模型(记为理论模型1)中的横隔梁宽度修改为40cm、高度不变,作为一个比较模型进行对比分析,记为理论模型2,并将按平面有限元模型(即按简化的弹性支承连续梁法计算其横向分布)计算的值及典型桥梁的试验实测值一并列入表1进行对比分析。

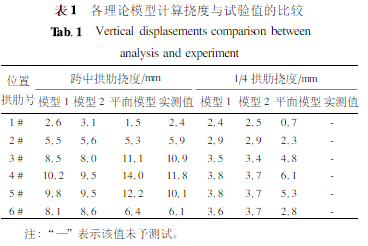
理论模型1与试验实测值的数据是基本相符的。主要的差异在于:在横向上,3#、4#拱片的跨中挠度实测值要比模型理论计算值大,而1#、6#实测挠度要小于理论值。观察桥梁实际结构,在试验荷载作用下,跨中3#、4#横隔梁有裂缝发展,尤其是4#,自下而上几乎贯穿多道裂缝,最大裂缝宽度为0.25mm,对于钢筋混凝土结构,裂缝的过度展开必 将导致变形的增大,从而减弱了荷载的横向传递,致使桥梁的跨中挠度在中间大于理论值、在两侧小于理论值,这是有一定道理的。

平面模型计算值与理论模型1、2的主要差别在于:简化的弹性支承连续梁法虽然可以大体上分配各拱片上承受的荷载,但不能考虑横向结构的强弱对结构整体产生的影响。空间模型反映了结构的在空间上的协同工作状态,比较空间模型与平面模型数据(尤其是1/4跨的数据),平面模型单纯按荷载分配系数 计算的结果与之存在巨大的差异,平面模型的误差是不可忽视的,存在明显的局限性。

理论模型2与理论模型1比较各拱肋的挠度在横向上的差异幅度减小。这是由于加 强了横隔梁,桥梁的横向联系得到加强,使得结构更好的协同工作。提取新模型的横隔梁分析结果,受力趋势与原模型一致,最不利单元仍为4#横隔梁上的21#单元,此时弯矩M=38.03kN・m,轴力F=514.76kN,针对这个荷载,通过加强配筋可以满足荷载要求。同时,拱架的最大主拉应力(位于4#拱架跨中附近,下缘)降低了1.3%,在一定程度上也体现了承载力的提高,但是不足以影响纵向结构的工程设计,因而可以认为空间分析的主要目的在于检验横向结构的强度。

5 结论

(1)传统的刚架拱桥的横向计算考虑不足使得横 向结构薄弱而导致结构的承载力下降,加强这类桥梁 的横向结构,使横向结构的刚度和强度与纵向结构相协调,可使桥梁更好地协同工作和提高其承载力。

(2)用传统的活载横向分布设计理论来计算纵向结构设计的荷载分配问题时,由于无法考虑横向结构的影响,不能对横向结构本身的结构设计提供理论指导,设计时存在较大的随意性和盲目性。为保证横向结构的安全合理,精确计算一般须建立空间有限元模型。笔者认为,在当前技术条件下,建立空间模型分析横向联系的内力并进行合理的设计是可行的,而且非常必要。